

Number systems
$\begin{gather*} \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \end{gather*}$
자연수 ⊂ 정수 ⊂ 유리수 ⊂ 실수
대수적 수 (Algebraic number)
정수 계수 다항방정식
$\begin{gather*} c_0x^d+c_1x^{d-1}+...+c_{d-1}x+c_d=0 \end{gather*}$
의 해가 되는 실수 및 복소수를 대수적 수(algebraic number)라고 한다.
ex)
유리수
√2 : x^2 - 2 = 0의 해다. ⇒ 대수적 수
√2 + √3 : 대수적 수간의 사칙연산은 마찬가지로 대수적 수다.
i = √-1
, ...
√2는 자연수 a, b에 대해 다음 디오판토스 근사가 가능하다.
$\begin{gather*} \left| \frac{a}{b} - \sqrt{2} \right| < \frac{1}{b^2} \end{gather*}$
이때,
$\begin{gather*} \frac{a}{b}+\sqrt{2} = \frac{a}{b}-\sqrt{2} +2\sqrt{2} < \frac{1}{b^2} + 2\sqrt{2} < 1 + 2\sqrt{2} \\ \Rightarrow \frac{1}{b^2} \leq \left| \frac{a^2-2b^2}{b^2} \right| = \left| (\frac{a}{b})^2-2 \right| < (1+2\sqrt{2}) \cdot \left| \frac{a}{b} - \sqrt{2} \right| \end{gather*}$
따라서
$\begin{gather*} \frac{1}{(1+2\sqrt{2})b^2} < \left| \frac{a}{b} - \sqrt{2} \right| < \frac{1}{b^2} \end{gather*}$
즉, √2는 1/b^2 보다 오차가 작은 좋은 유리수 근사(디오판토스 근사) a/b를 찾을 수 있지만,
상수 k = 1/(1+2√2)에 대해 최저 오차 k/b^2 보다 작게 근사할 수는 없다.
리우빌 Liouville
대수적 수 α (> 0)가 정수 계수 d차 다항식
$\begin{gather*} f(x)=c_0x^d+c_1x^{d-1}+...+c_{d-1}x+c_d=0, \ \ \ \ c_0 \not= 0 \end{gather*}$
의 해라면, 적당한 상수 k = k(α)에 대하여 다음 부등식이 항상 성립한다.
$\begin{gather*} \left| \frac{a}{b} - α \right| \geq \frac{k}{b^d} \end{gather*}$
즉, 대수적 수라면 최대 근사 속도가 존재한다. (그 값보다 오차가 작도록 근사할 수 없다.)
⇒ d차 방정식의 유리수 근사의 한계.
증명
By the mean value theorem(평균값 정리), there is c(b) with |α - c| < |α - (a/b)| such that
$\begin{gather*} f^\prime(c) = \frac{f(α) - f(a/b)}{α-(a/b)} = \frac{f(a/b)}{(a/b)-α} \end{gather*}$
Since deg(f(x)) = d, we have |f(a/b)| ≥ |(?)/b^d| ≥ 1/b^d
분자(: ?)는 항상 1 이상이다.
Therefore,
$\begin{gather*} \left| \frac{1}{f^\prime(c)} \cdot f(a/b) \right| = \left| \frac{a}{b} - α \right| \geq \left| \frac{1}{f^\prime(c)} \right| \cdot \frac{1}{b^d} \\ \geq \frac{1}{2|f^\prime(α)|} \cdot \frac{1}{b^d} = \frac{k}{b^d} \end{gather*}$
Finally, since the function f '(x) is continuous, |f '(c)| ≤ 2|f '(α)| if a/b is close enough to α.
Hence we get the wanted inequality with k(α) = 1/(2|f '(α)|)
초월수 (Transcendental number)
대수적 수가 아닌 실수.
리우빌의 부등식에 의하면, 임의의 자연수 d에 대해서 근사식 |a/b - α| < 1/b^d이 성립하는 유리수 a/b가 항상 존재하면 α는 초월수이다.
즉, 최대 근사 속도가 존재하지 않는다. (부등호가 리우빌 부등식에서랑 반대)
ex)
- Liouville's number : 0.101001000100001...
- π
- e
- Gelfond and Schneider : a^b is a transcendental number if a(≠ 0, 1) is a an algebraic number and b is an algebraic irrational number, such as
$\begin{gather*} \sqrt{2}^{\sqrt{2}} \end{gather*}$
- e^π = (-1)^(-i)
아직 모르는 거
- Are π ± e transcendental numbers? Are they irrational numbers? (At least one of them is a transcendental number.)
참고 1
$\begin{gather*} x = \sqrt{2}^{\sqrt{2}} \end{gather*}$
x는 무리수일까? 유리수일까?
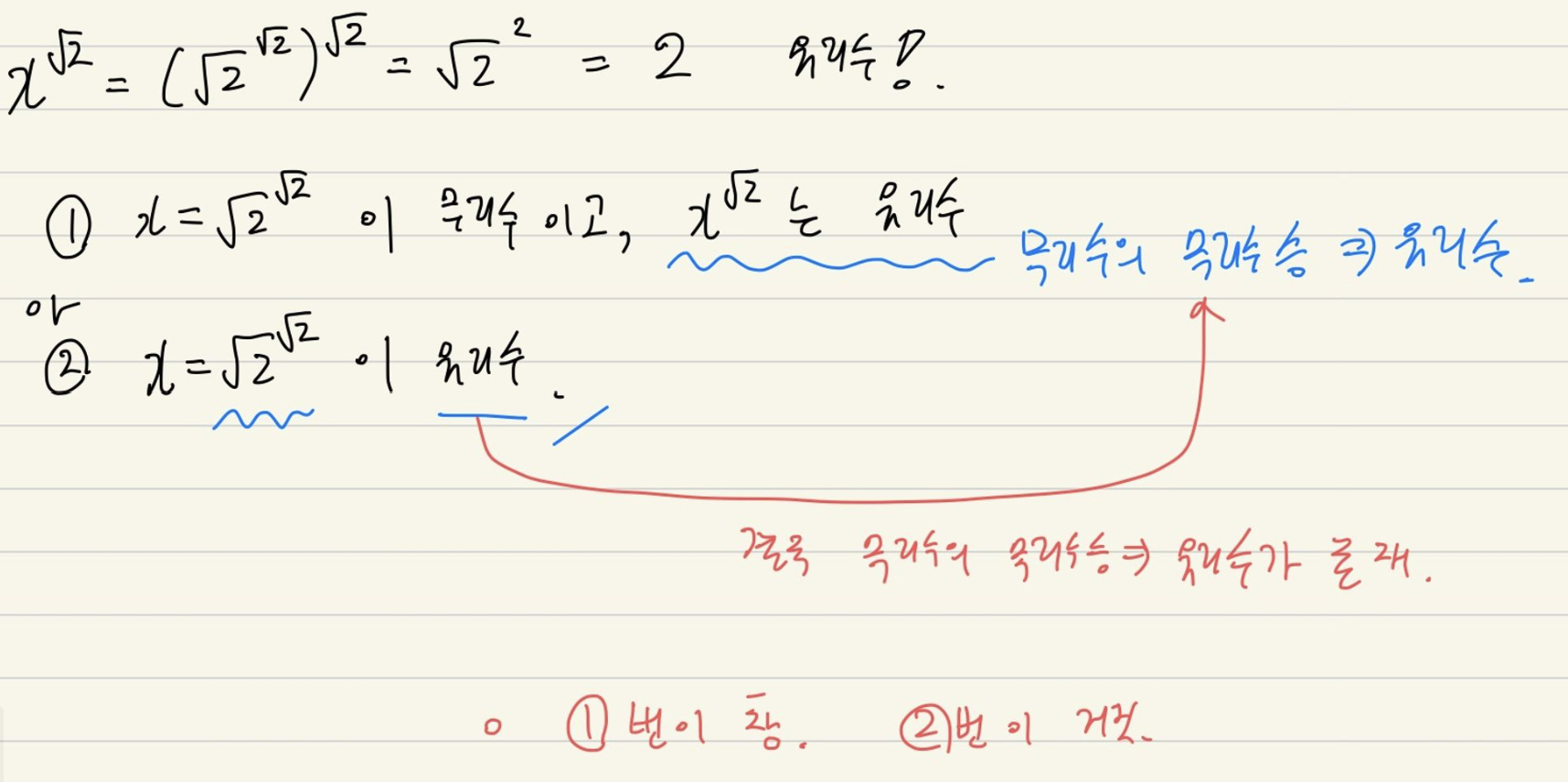
참고 2

참고 3

'CSE 학부 > 정수론' 카테고리의 다른 글
| 정수론 모음집 (0) | 2025.01.21 |
|---|---|
| 정수론 #10-3 :: 펠 방정식 일반화 (0) | 2025.01.21 |
| 정수론 #10-2 :: 디오판토스 근사 (0) | 2025.01.21 |
| 정수론 #10-1 :: 펠 방정식 (0) | 2025.01.21 |
| 정수론 #9 :: 페르마의 정리 (0) | 2025.01.21 |

틀린 부분은 언제든지 말씀해주세요!!! 감사합니다!

